IMPROVE Critical Orifice Flow Control
Author: Robert Eldred, CNL, University of California, Davis (raeldred@ucdavis.edu)
Date: May 4, 1998
The IMPROVE Critical Orifice Control System
Summary: The primary purpose of flow control is to keep the volume flow rate through the cyclone or PM10 inlet as close as possible to the nominal rate for the 2.5 or 10 µm cut. There are several factors producing a variation in the flow rate for a critical orifice: the diurnal and seasonal variation of ambient temperature, the change in pressure drop across the filter associated with variation in clean filters, and the change in pressure drop across the filter associated with mass loading. The estimated total variation in inlet flow rate with a critical orifice controller from all three factors is generally less than 3%. This is similar to the standard deviation in flow rates observed in the network. The conclusion is that a critical orifice system is reasonable if a variation in flow rate of approximately 3% is acceptable.
In the current IMPROVE sampler, the flow rate is measured before and after collection, but is not monitored during the sampling period. The secondary purpose of flow control is to assure that the measured flow rate represents the true average flow rate. That is, the flow controller must eliminate all unusual changes in flow rate during sampling. Measurements made at an eastern site in summer 1997 indicate that the flow rate behaves normally even with high mass loading and high relative humidity. In the new version of the IMPROVE sampler, to be installed during 1998, the flow rate will be monitored throughout the sampling period, making this purpose unnecessary.
The two major advantages of a critical orifice system is reliability and minimal maintenance. The reliability has been verified over the ten years of the IMPROVE network. The traditional mass flow control system is an unsatisfactory alternative, partly because it does not control the volume flow rate as well as a critical orifice system and partly because of high maintenance. The volume flow control systems proposed by several manufacturers for the FRM sampler appear to do an excellent job of controlling the volume flow rate. The maintenance requirements are less than with earlier mass flow systems, but still greater than with the critical orifice system. We have considered using a similar system, but have decided to wait until the reliability of these controllers has been verified in the FRM network. We will also wait to see if this method significantly increases the precision of the measurements.
I. Flow Rate and Particle Size Cut
Section I will examine the variation in flow rate for the IMPROVE sampler as it affects the particle size cut by the cyclone. The relationship between flow rate and the 50% aerodynamic diameter for the IMPROVE cyclone is
![]() , (1)
, (1)
On the other hand, the accuracy and precision of the air volume depends on how well the measured flow rates represent the true average flow rate, rather than how the flow rate compares to the nominal. Possible errors and uncertainties in volume will be discussed in Section II.
Equations: The volume flow rate at the critical orifice depends on the geometry of the orifice (primarily the diameter) and the square root absolute temperature of the air at the front of the orifice, but not on the pressure at the orifice:
Q'
= k *![]() ,
(2)
,
(2)
where k is a constant and Tc is the temperature at the critical orifice. Tests at Davis have shown no significant difference between the temperature at the cyclone and the temperature at the critical orifice. Therefore the subscript can be dropped.
The flow rate at the critical orifice differs from the volume flow rate at the inlet and cyclone because of the pressure across the filter. Because there is very little pressure drop across the cyclone, the volume flow rate after the cyclone is equal to the volume flow rate at the inlet. The volume flow rate at the cyclone is:
Q
= Q' * ![]() = k *
= k * ![]() , (3)
, (3)
where P is the decrease in pressure before the orifice and P is the ambient pressure.
To account for the pressure drop of the clean filter, each critical orifice is adjusted during calibration to give the desired flow rate with a typical clean filter appropriate for the module. If the nominal pressure drop used in calibration is Pcal, the flow rate during calibration is:
Qcal =
k * 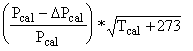 , (4)
, (4)
Combining Equations 2 and 3 and eliminating k, the flow rate is given by:
Q
= Qcal *
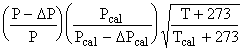 . (5)
. (5)
Expanding the pressure term and dropping terms beyond the second order:
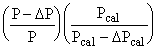 1 -
1 - ![]() = 1 -
= 1 - ![]() (6)
(6)
where P is the variation of the pressure drop from the nominal used in calibration.
The critical orifice controller is calibrated to provide a flow rate of 23 L/min for an ambient temperature of 20C and for the elevation of the site. (This yields a 2.5 µm cut point at 15°C.) The equation for the flow rate at the cyclone is then
Q = 23.0 *
![]() *
*![]() . (7)
. (7)
The pressure term of Equation 7 depends on the variation in the pressure drop across the filter from the nominal. There are two reasons for nonzero P: (1) the pressure drop for a given clean filter may vary from that of the nominal filter, and (2) the loading of the filter will increase the pressure drop. The variation in ambient pressure at the site is a lower order effect and can be safely ignored.
Variation in Pressure Drop for Clean Filters: The effect of the variation in clean filters can be estimated from the standard deviation of the pressure drops of the initial readings in the field. This was done for select sites during 1992 and 1997. For the PM2.5 Teflon and quartz filters, the resulting variation in flow rate was 0.7% and 1.4%, respectively, corresponding to a change in cut point of less than 0.1 m. The values for Teflon included both full 35 mm filter and those masked to 2.2 cm2. For the 47mm nylon filters used in 1992, the variation was 1.1%. In 1994, we shifted from 47mm to 25 mm filters. Recently there has been some quality control problems with nylon filters, producing a larger variation in pressure drop. Thus, in 1997, the variation increased to 3.9%. If quality control problems persist, we will shift back to 47 mm filters in the new version of the sampler. This larger uncertainty in the nylon flow rate will affect the IMPROVE concentrations for sulfate and nitrate. We have investigated the relationship between sulfate measured on nylon and sulfur measured on Teflon, comparing the period with 47 mm nylon with the period using 25 mm nylon. Figure 1 plots the distributions of the ratios of the difference between S*3 and SO4 for 1993 and 1997. Also shown is the theoretic fit expected for a Gaussian. If there had been a major shift in the uncertainty for sulfate on nylon, the 1997 distribution would become more spread out. The two years are nearly identical. The conclusion is that the change in the uncertainty in sulfate-on-nylon is too small to detect.
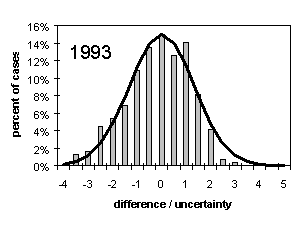
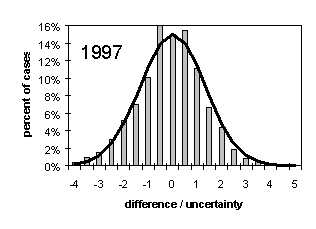
Figure 1. Distribution of the difference between the sulfate measured on Teflon (sulfur times 3) and sulfate measured on nylon. Also shown is the expected Gaussian fit. In 1993, the nylon filters were 47 mm, while in 1997 they were 25 mm.
Change in Pressure Drop because of Filter Loading: The filter loading pressure effect can be estimated from mean difference between the initial and final pressure drop readings for the same samples. For the Teflon and quartz filters, the effect on flow rate has generally been small: 1% for Teflon, and 0.1% for quartz. These small values were obtained with full 25 mm Teflon filters at eastern sites and with the collection area masked to 2.2 cm2 at most western sites. The effect was slightly larger for 25 mm nylon filters, 3% at most sites and 8% at Shenandoah and Dolly Sods.
Temperature Effects: The temperature effect in flow rate is proportional to the square root of the absolute temperature. Table 1 gives the variation in flow rate Q and d50 as a function of temperature, for the typical system in the IMPROVE network, which is calibrated to provide a cut point of 2.5 µm at 15°C, the median temperature for the IMPROVE network.
Table 1: Flow rate and 50% aerodynamic diameter vs. temperature
T (C) -20 -10 0 10 20 27 30 40
Q (L/min) 21.4 21.8 22.2 22.6 23.0 23.2 23.4 23.8
d50 (m) 3.0 2.8 2.7 2.5 2.4 2.3 2.3 2.2
For the entire network in 1997, the extreme temperatures at the time of the sample change ranged from -20°C to 40°C, the range used in Table 1. Eighty percent of the samples had temperatures between 0°C and 27°C, corresponding to cut points of 2.7 and 2.3 µm. In addition, we examined the variation in temperature at the Grand Canyon IMPROVE meteorological site for 1990; the standard deviation in absolute temperature over the year was 3.8%. Since the variation in flow rate depends on the square root of this, the standard deviation in flow rate was less than 2%.
Conclusions on the variation in flow rate: For the critical orifice the quadratic sum of pressure and temperature contributions give a total variation in flow rate of less than 3% for Teflon and quartz filters. The variation is also below 3% for 47mm nylon filters, but has recently risen to about 6% for 25 mm nylon, partly because of quality control in the filter material. In practice, the current critical orifice controllers maintain the flow rate as predicted. The mean measured flow rates for all PM2.5 samples for 6 years from March 1991 to February 1996 was 22.4 L/min with a standard deviation of 0.7 L/min (3%). This corresponds to a mean and standard deviation in d50 of 2.6 0.3 m.
II. Accuracy and Precision of Volume Calculation
The current method is to measure the flow rate before and after sample collection using two independent gauges. The mean flow rate during sampling is defined as the mean of the two values. The two major assumptions with this method are (1) the average temperature during sampling does not significantly vary from the temperatures at the two sample changes, and (2) the flow rate behaves reasonably. In 1998, the IMPROVE sampler will monitor the flow rate continuously. Thus, this section will no longer be applicable. It will also provide useful information to quantify the effect for the past 10 years.
Temperature Bias during Sample Change: If the average temperature during the two sample changes differs from the average temperature for the sampling period, the volume calculation will be incorrect. We examined 1990 Grand Canyon meteorological data, comparing the mean square root of absolute temperature for the Wednesday and Saturday sampling periods with those for various change hours on Tuesday. The largest single possible error for the year was less than 3%. There could be a systematic bias if the operator always changed samples during the warmest or coolest hours. If every change were done at 9 AM, there would be no difference for the means. The largest changes would have occurred if the changes were always performed at 2 PM; the error would be 0.6%. The conclusion is that the temperature assumption does not introduce significant error.
Unmeasured Fluctuations in Flow Rate: The assumption that the flow rate behaves reasonably throughout the sample collection can be verified using a data logger. This will be done for every sample in the modified IMPROVE sampler to be installed in 1998. One test was made at Dolly Sods Wilderness, WV, during summer 1997. This site ranks near the top in the IMPROVE network for both gravimetric mass and relative humidity. The primary purpose was to check that the pressure drop across the filter did not make any sudden changes because of high humidity. For example, a possible scenario is that the pressure drop for heavily loaded filters would suddenly increase rapidly as the RH approached 1. This was not observed.
Figure 2 gives the flow rates for modules A and B (Teflon and nylon), temperature, and relative humidity at Dolly Sods Wilderness, July 26, 1997. The mass concentration for this sample, 45 µg/m3, was the highest in the study. In 1997, only three samples in the entire network (all in the east) had higher concentrations. Since the flow rate was monitored on a sampler with a reduced collection area, an ambient concentration of 70 µg/m3 would be needed to give the same mass per unit area; no samples were at this level. Thus, this is an extreme case. While there is a steady decrease in flow rate as the filter loaded (6%), there was no unusual changes associated with high humidity. The average of initial and final flow rates differed from the true average by <1%.
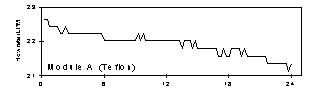
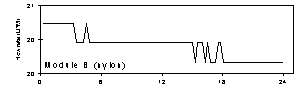
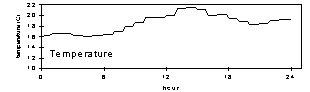
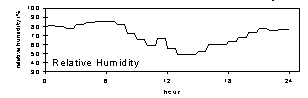
Figure 2. Flow rate for modules A and B (Teflon and nylon), temperature, and relative humidity at Dolly Sods Wilderness, July 26, 1997. The mass concentration for this sample, 45 µg/m3, was the highest in the study.
Figure 3 gives the same plots for July 26, 1997, which had the lowest mass concentration for the Dolly Sods study, 9 µg/m3. However, this is still a heavily loaded sample, above the median mass concentration for eastern sites, and larger than 93% of all samples at western sites. There is a smaller decrease in flow rate (3%) over the sampling period.
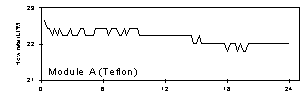
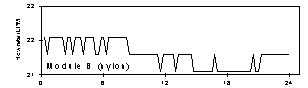
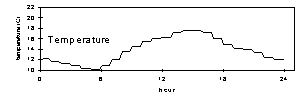
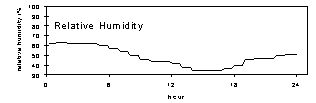
Figure 3. Flow rate for modules A and B (Teflon and nylon), temperature, and relative humidity at Dolly Sods Wilderness, July 30, 1997. The mass concentration for this sample, 9 µg/m3, was the lowest in the study.
Figure 4 gives the plots for the period with the highest average relative humidity in the study. The sample is heavily loaded compared to typical concentrations, corresponding the 97th percentile for eastern sites and 99th percentile for western sites. Once again there is no significant error in using the average of the initial and final readings compared to using the true average.
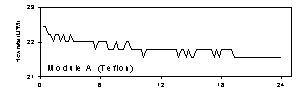
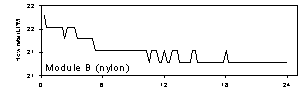
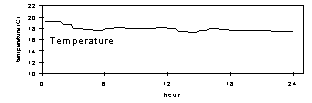
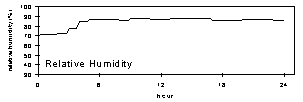
Figure 4. Flow rate for modules A and B (Teflon and nylon), temperature, and relative humidity at Dolly Sods Wilderness, August 13, 1997. The relative humidity was the highest in the study, at about 85% throughout the period. The temperature remained near 18°C throughout the period. The mass concentration for this sample was 17 µg/m3.
III. RELIABILITY, OPERATING CONDITIONS, AND MAINTENANCE
The critical orifice is a simple passive device that operates at all temperatures, that cannot lose its calibration, and that requires minimal maintenance. At the present time we are operating very efficiently, with a recovery rate of 95%. No samples have been lost because of the critical orifice.